
Die von der European Union Agency for Railways (ERA) seit dem Jahr 2010 grundsätzlich als Möglichkeit zur Berechnung von ETCS-Notbremskurven akzeptierte, stochastische Monte-Carlo-Methode birgt auch beachtliche Potenziale zur Modellierung der wechselseitigen Zusammenhänge innerhalb von Bremssystemen. Erweitert durch deren Regelkreise könnte sie im nächsten Schritt eine präzisere Berechnung der Bremskurven ermöglichen, sodass für ein gleiches Emergency Brake Confidence Level weniger Puffer in Form eines höheren Kdry_rst-Werts hinterlegt werden müsste. Dies würde – ohne Kompromisse bei der Sicherheit einzugehen – Potenziale für kürzere Zugfolgezeiten und in der Folge höhere Streckendurchsätze bieten. Um den potenziellen Nutzwert gerade vor dem zukünftigen ATO-Betrieb „auf die Schienen“ zu bringen ist allerdings eine Klärung der Integration der über die Monte-Carlo-Methode berechneten K-Werte in die geltenden Sicherheitsnachweise nötig.
80809 München
Deutschland
carina.smid@knorr-bremse.com

Quo Vadis, Monte-Carlo-Methode
Große Jachten, ein spektakuläres Formel-1-Rennen und Casinos – mindestens eins der drei dürften die meisten vor dem inneren Auge haben, wenn die Worte Monte Carlo fallen. In der Wahrscheinlichkeitsrechnung Bewanderte denken womöglich an ein nach dem Stadtstaat benanntes stochastisches Verfahren. Eines, das sehr häufig hintereinander Zufallsexperimente beschreibt. Theoretisch ließen sich diese Zufallsexperimente real durch Würfeln durchführen, was natürlich viel zu lange bräuchte. Deshalb werden die Zufallszahlen gemeinhin von Computerprozessoren generiert.
Die Methode eignet sich sehr gut zur Berechnung statistischer Mittelwerte und Abweichungen. Im Jahr 2006 wurde sie von der UIC zur Berechnung von ETCS-Notbremskurven vorgeschlagen [1] und vier Jahre später von der European Union Agency for Railways (ERA) als Möglichkeit akzeptiert [2]. Darüber hinaus bietet sich die Methode jedoch auch an, um nicht mehr nur entlang einer Hierarchieebene im Bremssystem Aussagen zu dessen Ausfallwahrscheinlichkeiten und Leistungsstreuung zu geben, sondern sie bereits bei der Auslegung von Bremssystemen in deren Regelkreis einzusetzen. Somit ließen sich einerseits schon zu diesem sehr frühen Zeitpunkt in der Entwicklung Aussagen über die im Betrieb notwendigen ETCS-Bremskurven treffen – andererseits auch die Bremskurven selbst präziser berechnen.
Zusammenfassung
Die von der European Union Agency for Railways (ERA) seit dem Jahr 2010 grundsätzlich als Möglichkeit zur Berechnung von ETCS-Notbremskurven akzeptierte, stochastische Monte-Carlo-Methode birgt auch beachtliche Potenziale zur Modellierung der wechselseitigen Zusammenhänge innerhalb von Bremssystemen. Erweitert durch deren Regelkreise könnte sie im nächsten Schritt eine präzisere Berechnung der Bremskurven ermöglichen, sodass für ein gleiches Emergency Brake Confidence Level weniger Puffer in Form eines höheren Kdry_rst-Werts hinterlegt werden müsste. Dies würde – ohne Kompromisse bei der Sicherheit einzugehen – Potenziale für kürzere Zugfolgezeiten und in der Folge höhere Streckendurchsätze bieten. Um den potenziellen Nutzwert gerade vor dem zukünftigen ATO-Betrieb „auf die Schienen“ zu bringen ist allerdings eine Klärung der Integration der über die Monte-Carlo-Methode berechneten K-Werte in die geltenden Sicherheitsnachweise nötig.
Bisheriger Einsatz der Methodik
Angewendet auf Bremssysteme von Schienenfahrzeugen ist die Monte-Carlo-Methode in der Lage, die statistische Verteilung bremsrelevanter Eigenschaften sowie deren Einfluss auf die Bremsperformance zu beschreiben. Dabei berücksichtigt sie Ausfall- und Abweichungswahrscheinlichkeiten von Parametern mit Einfluss auf die Bremsperformance.
Ausgangspunkt hierfür ist bislang ein Hierarchiemodell, dass die Auswirkungen einer Reihe von Parametern mathematisch modelliert. Im Wesentlichen handelt es sich dabei um solche zur Architektur des Bremssystems bestimmenden Parameter. Beispielsweise zu nennen sind Wagen oder Drehgestell selektive Bremsansteuerung, die Streuung der Kennwerte einzelner Bremssystemkomponenten (Zylinderdrücke, Gestängewirkungsgrade, Reibwerte), die Zuverlässigkeit und Ausfallwahrscheinlichkeit der einzelnen Systemkomponenten, die Abhängigkeiten der Systemkomponenten untereinander sowie einzelne Funktionen des Bremssystems. Für Letzteres steht etwa die sogenannte Hoch-Niedrig-Abbremsung im Hochgeschwindigkeitsbereich.
Da das Modell die bremsrelevanten Eigenschaften mit ihren statistisch auftretenden Wahrscheinlichkeiten verknüpft, öffnet es auch die Option einer zusätzlichen Anwendung: Das Einfügen beliebiger zufälliger Werte der Eigenschaften zur Simulation des zufälligen Verhaltens des Bremssystems [3].
Integration von Bremssystemregelkreisen in die Monte-Carlo-Methode
Das gleiche Prinzip lässt sich nun auch für die wechselseitigen Zusammenhänge innerhalb des Bremssystems durchführen. Etwa, ob sich die Parameter-Abweichung oder gar der Ausfall einer Komponente funktional auf weitere Komponenten überträgt.
Den Ausgangspunkt hierfür generiert das Monte Carlo-Modell selbst: Es „würfelt einen beliebigen vom gewünschten Zustand abweichenden Zustand. Dieser Zustand wird daraufhin wie im konkreten Bremssystem ausgeregelt. Gespeichert wird abschließend der sich einstellende ausgeregelte Endzustand. Dieser „Würfel”/Regelzyklus (Bild 1) wiederholt sich in der Größenordnung von 10 bis 100 Milliarden Rechenzyklen – solange, bis die Korrekturfaktoren aller gewünschten Vertrauensbereiche (EBCL) ermittelt wurden.
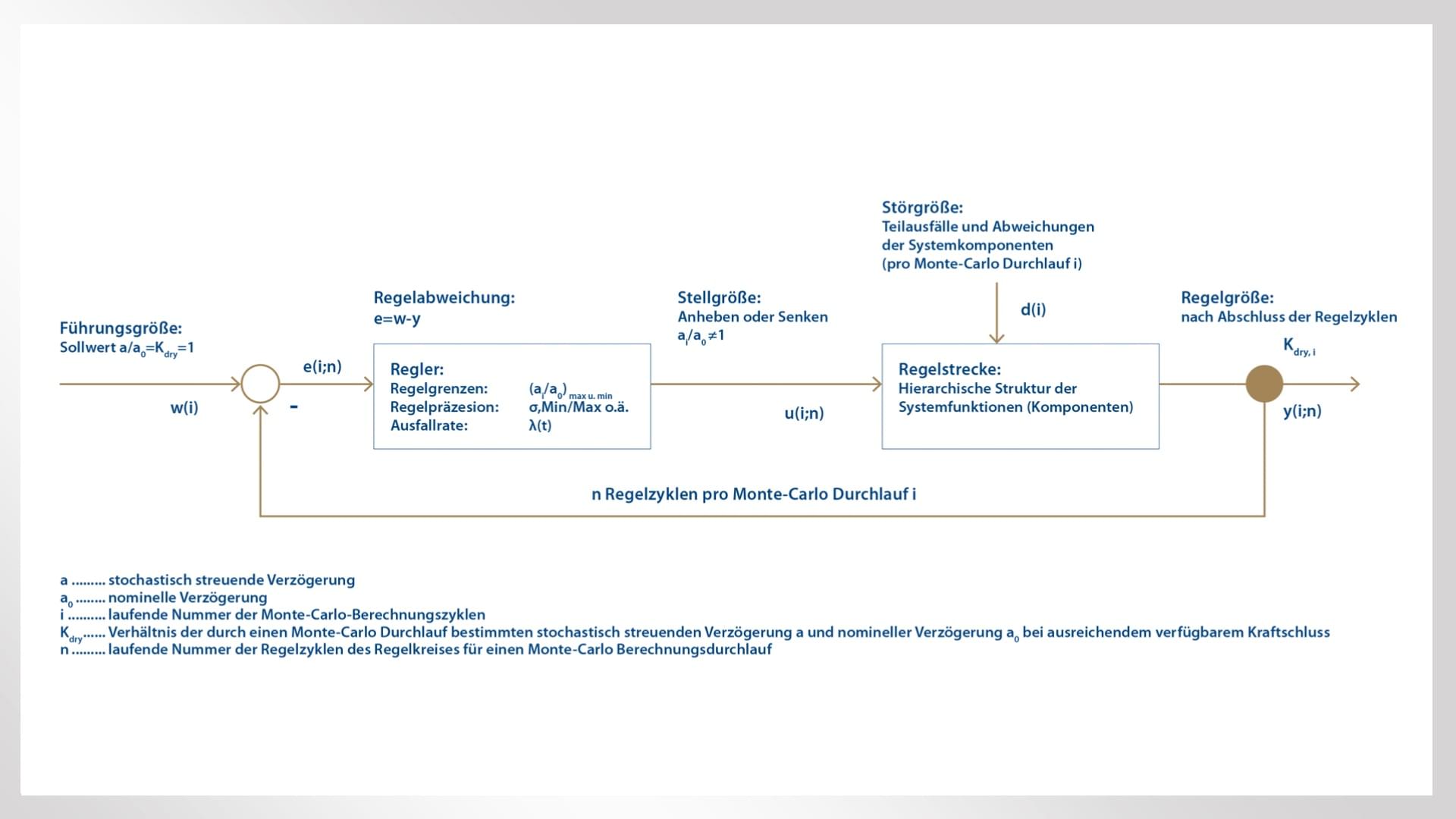
Auf gleiche Weise kann die Monte-Carlo-Simulation nun für praktisch alle denkbaren Komponentenausfälle (sowie deren Kombination untereinander) den fahrzeug- oder zugverbandsspezifischen Korrekturfaktor Kdry_rst berechnen. Dieser wird für die verschiedenen betriebsseitig geforderten EBCLs (Emergency Brake Confidence Level, dt.: Vertrauensniveaus) geschwindigkeitsabhängig festgelegt und setzt die Verzögerung eines Bremssystems in einem bestimmten Zustand ins Verhältnis zur nominalen Verzögerung. Wie in der Vergangenheit liefern die Kdry_rst-Werte auch weiterhin die Datenbasis an die ETCS Onboard Unit zur Bestimmung der betrieblichen Bremskurven – allerdings basieren die Werte nicht auf formal definierten Toleranzen. Stattdessen werden sie mithilfe der Monte-Carlo-Methode entlang der Eintrittswahrscheinlichkeiten der konkreten Bremssystemzustände ermittelt.
Wichtig zum Verständnis des Gesamtzusammenhangs: Im Sinne des UIC- Vorschlags aus dem Jahr 2006 bewertet „Monte Carlo“ Ausfallwahrscheinlichkeiten von Bremssystemkomponenten in Beziehung zur erwartbaren Bremsleistung, wenngleich es keine Bewertung über die formal erreichbare Sicherheitsintegrität abgibt. Wohl aber quantifizieren die Ergebnisse nun schon im Designprozess des Bremssystems die Bremsperformance, sodass ein Zug mit gut begründeten Sicherheitsmargen beaufschlagt werden könnte. Werden konventionell gesteuerte Bremssysteme durch Regelzyklen erweitert – und diese auch in der Monte Carlo Simulation mit berücksichtigt – sind geringere, notwendige Sicherheitsmargen respektive „bessere“ EBCL-Kurven für die Möglichkeit einer Verdichtung des Schienenverkehrs zu erwarten (Bild 2).
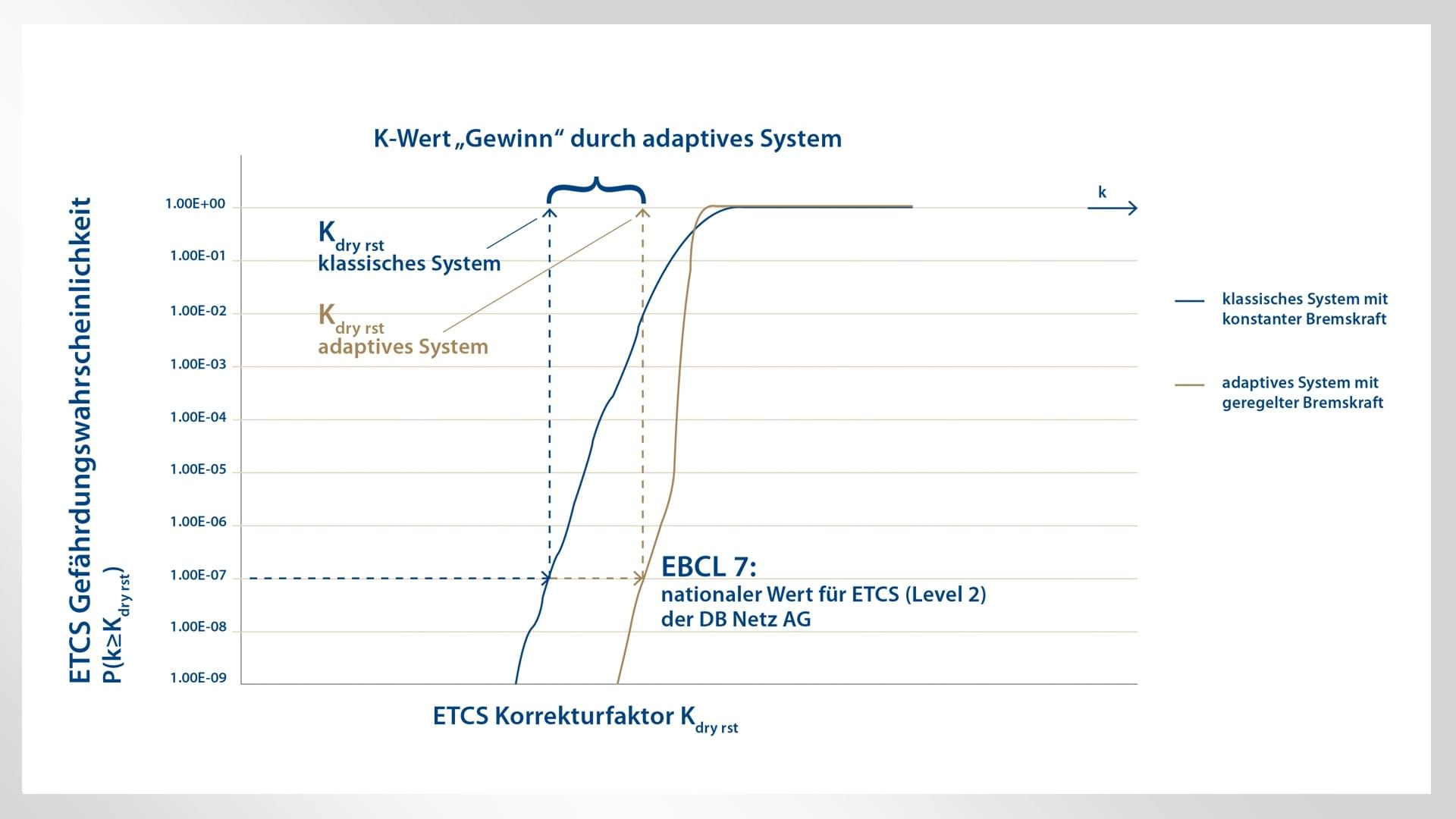
Gewinnbringender Einsatz der Methode bei der Auslegung von Bremssystemen
Dieser nun auch die Wechselwirkungen zwischen den einzelnen Bremssystemkomponenten berücksichtigende Weg generiert in mehreren Punkten attraktiven Mehrwert: Zum einen wäre Entwicklern mit den Monte-Carlo-generierten Kdry_rst-Werten eine modulare Auslegungsunterstützung zur Hand gegeben, wo sie bislang noch auf eine bestimmte definierte Bremssystemarchitektur beschränkt waren. Zum anderen könnte die Monte-Carlo-Methode sie bei der Berechnung des dynamischen Bremsverhaltens unterstützen – und damit auch konkret beziffern, inwieweit sich der angenommene Ausfall einer beliebigen Systemkomponente von einer anderen im Zug verfügbaren Bremsfunktion belastbar kompensieren ließe.
Im Umkehrschluss führen die präziser berechneten Bremskurven dazu, dass für gleiches Emergency Brake Confidence Level nunmehr weniger „Puffer“ in Form eines höheren Kdry_rst-Werts hinterlegt werden müsste. Die Belastbarkeit der Herangehensweise in Form von Sicherheitsnachweisen entsprechend validiert, könnten Züge ohne Abstriche bei der Sicherheit enger getaktet fahren und damit den Durchsatz eines bestimmten Streckenabschnitts steigern.
Gesamtzusammenhang und Ausblick
An diesem Punkt spielt die Methode direkt in die Ziele einer Reproducible Braking Distance (RBD) hinein. Diese betrachtet Verzögerungsregelung, Gleitschutz und Kraftschluss-Management innerhalb eines Bremssystems aus integrierter Perspektive und zielt darauf ab, Varianz und Streuung von Bremswegen auch unter ungünstigen Bedingungen deutlich zu reduzieren. Bei trockenen Schienen – und allen voran aufgrund der geringeren Bremswegstreuung – hatten Simulationsrechnungen teils signifikante Spannen für verkürzte theoretische Zugfolgezeiten ergeben: 9 bis 19 % bei U-Bahnen, 9 bis 16 % bei S-Bahnen, 1,5 bis 4 % im Regionalverkehr mit Triebzügen sowie bis zu 20 % im (chinesischen) Hochgeschwindigkeitsverkehr (Tabelle 1) [4].
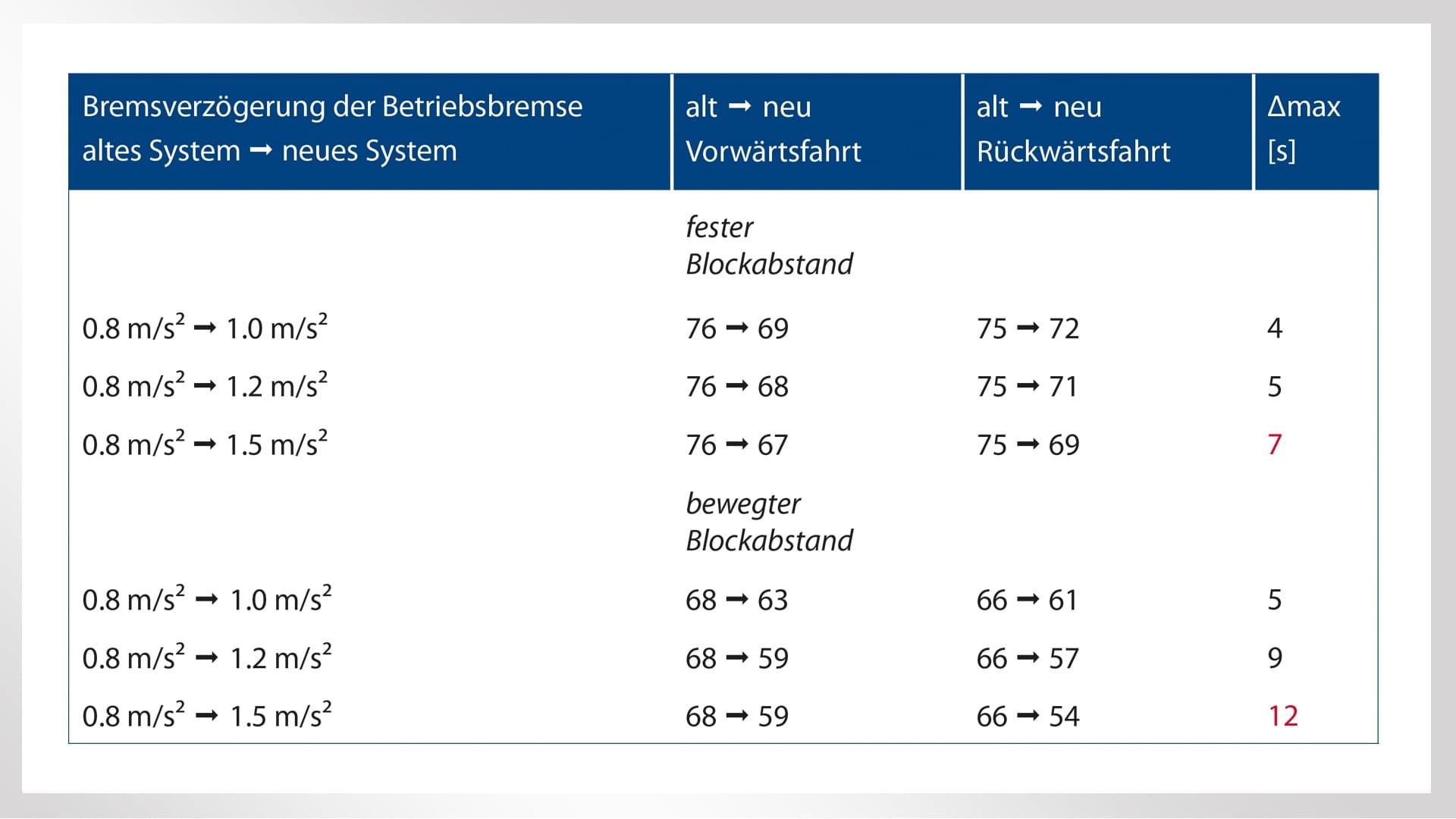
Auch den Kwet-Wert als ETCS-Korrekturfaktor unter nassen Schienenbedingungen reduziert der Ansatz deutlich. Muss für einen sicheren Betrieb mit konventionellen Bremssystemen die Verzögerung unter nassen Schienenbedingungen um bis zur Hälfte reduziert werden, reicht mit einem RBD-erhöhten Faktor Kwet eine Reduzierung um lediglich ein Drittel aus [4]. An dieser Stelle könnte die Monte Carlo-Methode den sprichwörtlichen Kreis schließen – indem sie einzelnen Bremsfunktionalitäten und ihre Zuverlässigkeit in den RBD-Kontext einbindet.
Allein: Um den potenziellen Nutzwert dieser Herangehensweise gerade vor dem zukünftigen ATO-Betrieb „auf die Schienen“ zu bringen ist eine Klärung der Integration der über die Monte-Carlo-Methode berechneten K-Werte in die geltenden Sicherheitsnachweise nötig.
Autor: Dipl-Ing. Ernst Hohmann
Literaturverzeichnis:
[1] UIC B 126/DT414: Braking Questions – Methodology for the safety margin calculation of the emergency brake intervention curve for trains operated by ETCS/ERTMS, June 2006.
[2] Calcul de facteurs de correction pour utilisation comme données d’entrée ERTMS Référence affaire : n° 09-0164, Référence : P/CIM ESF2/2010-0885, Version 2 du 28/04/2010.
[3] Horn, S.; Pavlović, O.: Chancen und Möglichkeiten der Monte-Carlo-Methode bei der Bestimmung der ETCS-Bremskurven. ETR September 2017.
[4] Englbrecht, M.; Gremmel, H.; Hohmann, E.; Linke, T.; Höhere Transportkapazitäten auf der Schiene: Simulation zeigt Potenziale für optimierte Auslastung bestehender Infrastruktur. ZEVrail 144 (2020) 8, S. 276-281.